G Berechnung von Schienenspannungen: Unterschied zwischen den Versionen
Lutz (Diskussion | Beiträge) |
Lutz (Diskussion | Beiträge) |
||
| Zeile 88: | Zeile 88: | ||
stecke ich das alles in Variablen und gebe bei dem Iterationsschritt die entsprechende Tabelle aus. | stecke ich das alles in Variablen und gebe bei dem Iterationsschritt die entsprechende Tabelle aus. | ||
So bekommt man eine prüfbare Kontrolle bzgl. der Federsteifigkeiten. | So bekommt man eine prüfbare Kontrolle bzgl. der Federsteifigkeiten. | ||
ungefähr so: | |||
[[Datei:Nonl federn.jpg|gerahmt|links|Struktur der nichtliniearen Federn]] | |||
== Normen == | == Normen == | ||
Version vom 25. November 2022, 12:42 Uhr
Allgemeines
Bei der nichtlinearen Berechnung der Schienenspannungen handelt es sich um eine eisenbahnspezifische Aufgabenstellung. Bezeichnenderweise ist eine Berechnung per Hand nicht möglich.
Eingangsgrößen
Gleis
- Anzahl der Gleise
- mögliche Fahrtrichtungen auf den Gleisen
- Gleisachse (ggf. Bogenatmung)
- Gleisoberbau (Schotter, Schienen, Schwellen, Schienenbefestigung mit reduzierten Durchschubwiderstand, ggf. Schienenbefestigungen mit freiem Durchschub)
Belastung
- Lastmodelle (vertikal und horizontal) bzw. Streckenklasse·
- Klassifizierungsfaktor (nur für belastete Gleise)
- dynamischer Beiwert
- Zuglänge
- Temperatur (nur Überbau, nicht die Schienen)
- ggf. Kriechen und Schwinden
Bei der Belastung gibt es immer wieder unterschiedliche Auffassungen, ob aus dem LM 71 nur die Streckenlast oder auch die "Loklast" zu berücksichgen ist. Dann muss man aber auch über die Widerstandsgesetze (gelten für 80kN/m) nachdenken. Auch die Frage, ob nur auf dem Überbau oder auf der gesamten Länge Bremskräfte wirken, beantwortet die Norm nicht verbindlich. Der Reduktionsfaktor ξ ist nicht zu berücksichtigen; er sollte eines der Ergebnisse sein.
- Läsverschiebewiderstand (belastet bzw. unbelastet); bei "belastet" mit Klassifierungsfaktor α[1]
Hier muss ggf. mit dem Prüfer geklärt werden, ob bei den Lastmodell SW/0 und SW/2 größere Widerstandswerte einzurechnen sind. Die Werte im Bild 4 gelten für das LM71. Überbau
- statisches System
- Stützweite bzw. Ausgleichslänge
- Material
- Steifigkeit
Unterbauten
- Steifigkeit K
- Bodengutachten (ggf. dynamische Steifigkeit des Baugrunds)
Geometrie
- Konstruktionshöhe
- Höhe des Oberbaus
Literatur
Zum Thema "Berechnung von Schienenspannungen" liegt nachstehende Literatur vor:
- Handbuch Eisenbahnbrücken, Abschn. 4.2 und 10.4
- Handbuch Entwerfen von Eisenbahnbrücken, Abschn. 10.4
- Menge, Petrascheck; Interaktion Gleis - Tragwerk - Entwurfskriterium der Steyrtalbrücke, Bauingenieur , April 2013, (Q1)
- ThyssenKrupp GfT Gleistechnik, Oberbauhandbuch
Der VDEI gibt ebenfalls eine Publikation zu diesem Thema heraus.
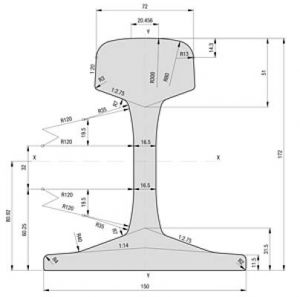
klassisches Schienenprofil
Die in der Norm (Handbuch EC 1, Abschn. 6.5.4.5.1) angegeben zulässigen Spannungen gelten nur für das Profil UIC 60!
Ziele der Berechnung
Im Sommer besteht die Gefahr von Gleisverwerfungen, im Winter von Schienenbrüchen. Deshalb:
- Ermittlung der zusätzlichen (charakteristischen) Schienenspannungen
- Nachweis der Verformungen
- ggf. Nachweis der Abhebekräfte
- Berechnung der Lasteinleitung in die Unterbauten
Modellbildung
Allgemeines
Bei der Modellierung ist zu beachten:
- die Federsteifigkeit K sollte gf. variiert werden
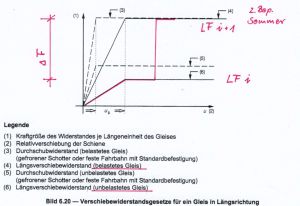
- es sind zwei Jahreszeiten zu betrachten, was auch unterschiedliche Verschiebewiderstandsgesetze zur Folge hat
- die unterschiedlichen Laststellungen erfordern ebenfalls unterschiedliche Verschiebewiderstandsgesetze
- für die durchgehenden Schienen genügt es, Fachwerkstäbe zu modellieren
- der Brückenüberbau ist ein Biegeträger
- besonders wichtig ist die korrekte Erfassung der vertikalen Abstände (Drehachse der Lager – Schwerachse Überbau – Schwerachse Schienenprofil)
- die Federrichtung kann man recht gut über das lokale Koordinatensystem und den Federtyp steuern
Sinnvollerweise beträgt der Abstand zwischen den einzelnen Laststellungen ein ganzzahliges Vielfaches der Elementteilung. Gleiches gilt für die zu betrachtende Zuglänge. Für die Elementteilung sollte ein Meter (nicht der tatsächliche Schwellenabstand) angesetzt werden. Querschnittswerte der einzelnen Schienenprofile findet man im Oberbauhandbuch der Firma GfT Gleistechnik. Die DIN EN 1991-2 zeigt im Bild 6.19 ein mögliches Modell.
Gelegentlich werden die Dammbereiche im Modell lediglich über eine "Anschlussfeder" simuliert; dass ist aber in unserem Zeitalter nicht mehr notwendig.
nichtlineare Berechnung und nichtlineare Überlagerung
Ein Feder hat bei jeder Belastung eine Federkraft und einen Federweg. Wenn nun die Federsteifigkeit zwischen zwei Lastfällen verändert wird und der vorherige Lastfall zugleich der Primärlastfall ist, stellt sich die Frage, ob die Federkraft und / oder der Federweg übernommen wird. eigene Test!
Weiterhin ist zu beachten, daß sich aus dem Wechsel der Federarbeitslinie aus dem vorherigen Primärlastfall in der Feder (Schiene) eine neue Federkraft einstellt!
Die Norm erlaubt es, dass man die unterschiedlichen Einwirkungen (also erst die Temperatur und dannach die Vertikallasten und das Bremsen/Anfahren) nichtlinear berechnet und als unabhängige Größen anschließend linear überlagert [2]. Diese Vorgehensweise liefert Ergebnisse auf der unsicheren Seite. Besser ist es, die Berechnung mit sogenannten Primärlastfällen durchzuführen und die Belastungsgeschichte korrekt abzubilden.
Generierung der Federn
Für das nächste Mal:
- jeder Knoten (jede Schwelle: Achtung Schwellenabstand) bekommt eine eigene smat_Nr. Das ist vor allem für die Modelle SW/0 und SW/2 ratsam.
- Unterscheidung zwischen Sommer und Winter
- Unterscheidung zwischen unbelastet und belastet (ggf. mit Klassifizierungsfaktor)
stecke ich das alles in Variablen und gebe bei dem Iterationsschritt die entsprechende Tabelle aus. So bekommt man eine prüfbare Kontrolle bzgl. der Federsteifigkeiten.
ungefähr so:
Normen
Die RiL 804.3401 Abschn. 8 Bild 4 gibt Werte für die nichtlinearen Arbeitslinien vor. Diese können auch für Behelfsbrücken angesetzt werden. Hier muss zwischen Längsverschiebewiderstand und Durchschubwiderstand unterschieden werden.
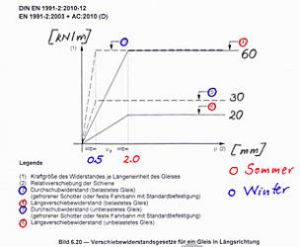
- DIN EN 1991-2 Abschn. 6.5.4 (Achtung! die Abschn. 6.5.4.5 und 6.5.4.6 sind durch die RiL 804.3401 aufgehoben); auch der Anhang G des EC 1 sollte nicht angewandt werden.
- Richtlinie 804.3401
- Richtlinie 804.4110 Abschn. 6
Kontrolle, Kontrolle, Kontrolle!
Die nichtlineare Berechnung von Schienenspannungen ist eine ziemlich komplexe Angelegenheit. Das verwendete Modell liefert vielleicht auch unerwartete Ergebnisse! Deshalb sollte man sich einfache Lastfälle zum Testen des Modells überlegen und die so gewonnenen Ergebnisse auf Plausibilität prüfen. Manches Zwischenergebniss kann man auch zahlenmäßig kontrollieren.
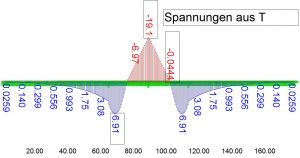
Kontrolllastfall T
Bei einem symmetrischen System müssen die Temperaturlastfälle symmetrische Schnittgrößen ergeben.
fiktive Horizontalkraft
Eine gute Kontrolle besteht in der Untersuchung einer Horizontalkraft im Überbau. Dabei erkennt man die Verteilung dieser Last auf die Festlager (wenn es mehrere gibt). Ab einer bestimmten Lastgröße sollten auch die Federn nichtlinear reagieren. Weiterhin erkennt man die Übertragung der Last vom Überbau auf die Schiene, so zu sagen "entgegengesetzt".

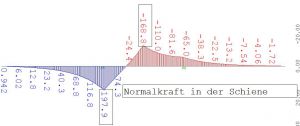
Ebenfalls eine gute Kontrolle ist eine Kraft, aber nicht am Überbau, sondern in der Schiene.
Behelfsbrücken
In der RiLi 804.4110 Abschn. 7 (Auflagerkonstruktionen und Lager), Absatz 11 wird geregelt, was bei Baubehelfen zu planen ist. Ab 30m Gesamtlänge wird eine UiG erforderlich und es sind die Schienenspannungen... nachzuweisen.[3]
Schlagwörter
Schienenspannungen, Schienen, Neudefinition der Federkennwerte, Kontrolle der Federarbeitslinien