C Neudefinition von Federkennwerten

Neudefinition von Federkennwerten

Bei nichtlinearen Berechnungen werden häufig die Federn im Laufe der Berechnung "umdefiniert". So sind bei der Berechnung von Schienenspannungen die horizontalen Federn unter den Schienen bei Nichtbelastung deutlich weicher, als wenn der Zug auf dem Gleis steht. Dementsprechend müssen die Federn entsprechend der aktuellen Laststellung dann neu festgelegt werden.

zwei Fließniveaus

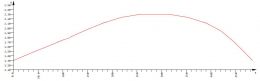
Es kann sowohl bei der weichen Feder als auch bei der harten Feder zum Fließen kommen. Um das für eine konkrete Feder zu kontrollieren, lässt man sich im WINGRAF die Federwege und die Federkraft ausgeben. Da die Federwege unbegrenzt festgelegt wurden, können hier sehr große Verschiebungen auftreten, wohingegen bei der Federkraft die Deckelung wirkt.

Die Grafiken zeigen die beiden klassischen Fälle:

• die Temperaturbeanspruchung führt nocht nicht zum Fließen der weichen Feder; es wird nun umgeswitcht auf die steife Feder; die nachfolgende Belastung bringt nun aber diese Feder zum Fließen
• bereits die Temperaturbeanspruchung führt zum Fließen der weichen Feder; nach der Neudefinition steigen die Verschiebungen erst linear und dann aber wieder nichtlinear weiter an

In beiden Fällen ist die errreichte Federkraft gleich groß. Im zweiten Fall treten (hier) größere Verschiebungen auf.

• 

  komplettes System

• 

  Eigengewicht ohne großes Feld

• 

  Verlauf der Höhe über die Stationierung

• 

  Querschnitt