C Parametrisierung und Variantenuntersuchung: Unterschied zwischen den Versionen
Lutz (Diskussion | Beiträge) |
Lutz (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (22 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Vorbemerkungen == | == Vorbemerkungen == | ||
Mittels der Parametrisierung (bei textbasierter Eingabe) lassen sich schnell und sicher die Eingangsgrößen einer Berechnung varieren. Wesentlich ist dabei, dass man wirklich '''an allen Stellen''', wo der Paramter in die Berechnung eingeht, auch tatsählich diesen Parameter verwendet. | Mittels der Parametrisierung (bei textbasierter Eingabe) lassen sich schnell und sicher die Eingangsgrößen einer Berechnung varieren. Wesentlich ist dabei, dass man wirklich '''an allen Stellen''', wo der Paramter in die Berechnung eingeht, auch tatsählich diesen Parameter verwendet. | ||
Die Parametrisierung ist die Voraussetzung für Variantenuntersuchungen. | Die Parametrisierung ist die Voraussetzung für Variantenuntersuchungen. | ||
'''Aufgepasst!''' | '''Aufgepasst!''' | ||
Man beachte auch, dass eine lokale LET-Variable eine gleichnamige globale STO-Variable überschreibt!!! | |||
Da das Programm keine Warnung bei der Überschreibung einer STO-Variable gibt, kann man natürlich echten Blödsinn fabrizieren. 👀 | Da das Programm keine Warnung bei der Überschreibung einer STO-Variable gibt, kann man natürlich echten Blödsinn fabrizieren. 👀 | ||
Wenn zum Beispiel sto#w 65 die Brückenschiefe definiert und man zwischendurch mal die Windlast mit let#w 2,6 festlegt, dann ist es passiert. Falls man anschließend sin(#w) verwendet, um aus der Brückenschiefe etwas abzuleiten, so ist das Ergebnis sehr wunderlich! Hier hilft, für die Variablen länger Namen zu verwenden: #w_schiefe und #wind. | Wenn zum Beispiel sto#w 65 die Brückenschiefe definiert und man zwischendurch mal die Windlast mit let#w 2,6 festlegt, dann ist es passiert. Falls man anschließend sin(#w) verwendet, um aus der Brückenschiefe etwas abzuleiten, so ist das Ergebnis sehr wunderlich! Hier hilft, für die Variablen länger Namen zu verwenden: #w_schiefe und #wind. | ||
Das klingt alles ganz gut???! hat aber auch seine Haken. Man kann z.Bsp. eine Variable mit sto#variable in die Datenbank schreiben. Dann verwendet man diese...alles prima. Aber wir Statiker wollen ja alles x-mal ändern. Also verwenden wir eine andere Variable sto#variable_neu! Leider haben wir '''zwischenzeitlich vergessen''', dass wir die alte Variable an mehreren Stellen verwendet haben. Nun kommt das große Staunen. 🤔 regelmäßig die DATENBANK LÖSCHEN!!!! | |||
Da man bei integralen Brücken die unterschiedlichen Grenzwerte Bodensteifigkeiten betrachten muss, sind diese Bauwerke nur mittels Parametrisierung berechenbar. | Da man bei integralen Brücken die unterschiedlichen Grenzwerte Bodensteifigkeiten betrachten muss, sind diese Bauwerke nur mittels Parametrisierung berechenbar. | ||
| Zeile 13: | Zeile 16: | ||
== Parametrisierung bei ähnlichen Bauteilen == | == Parametrisierung bei ähnlichen Bauteilen == | ||
[[Datei:Parameter.jpg|gerahmt|rechts|ähnliche Bauteile]] | [[Datei:Parameter.jpg|gerahmt|rechts|ähnliche Bauteile]] | ||
Bei ähnlichen Bauteilen (Tunnelquerschnitte, Schächte, Tröge, Fertigteile) bietet es sich an, die Berechnung in einer '''Zentraldatei''' durchzuführen. | Bei ähnlichen Bauteilen (Tunnelquerschnitte, Schächte, Tröge, Fertigteile, [[G Lärmschutzwände auf Bahnbrücken|Lärmschutzwände]]...) bietet es sich an, die Berechnung in einer '''Zentraldatei''' durchzuführen. | ||
Neben der Geometrie werden auch die Lasten über Parameter erfasst. | Neben der Geometrie werden auch die Lasten über Parameter erfasst. | ||
Für jedes einzelne Bauteil wird dann nur eine kleine Steuerdatei erzeugt, in welcher die konkreten Parameter definiert werden. | Für jedes einzelne Bauteil wird dann nur eine kleine Steuerdatei erzeugt, in welcher die konkreten Parameter definiert werden. | ||
| Zeile 70: | Zeile 73: | ||
spt nr 300+#nr x #x_teller(#nr) y #bg+#ly-#y_teller z #z2-#z_teller fix 'pypz' nx 0 ny 0 nz 1 sx 1 sy 0 sz 0 | spt nr 300+#nr x #x_teller(#nr) y #bg+#ly-#y_teller z #z2-#z_teller fix 'pypz' nx 0 ny 0 nz 1 sx 1 sy 0 sz 0 | ||
endloop | endloop | ||
== Parametrisierung eines Verbundquerschnitte == | == Parametrisierung eines Verbundquerschnitte == | ||
Im Stahlverbundbau ist Parametrisierung ein "Muss". Besonders die Blechdicken und die Trägerhöhen dienen der Anpassung des Widerstands an die Beanspruchung. | Im Stahlverbundbau ist Parametrisierung ein "Muss". Besonders die Blechdicken und die Trägerhöhen dienen der Anpassung des Widerstands an die Beanspruchung. | ||
| Zeile 146: | Zeile 150: | ||
Mit dem CABD kann man das aber noch etwas eleganter erledigen. | Mit dem CABD kann man das aber noch etwas eleganter erledigen. | ||
== Parametriesierung mit CABD == | == Parametriesierung mit CABD == | ||
[[Datei:Parametrisierter querschnitt.JPG|mini|rechts|parametrisierter Querschnitt]] | |||
<center><pdf>File:Parametrisierter querschnitt teddy.pdf</pdf></center> | |||
Mit dem CABD - Werkzeugen kann man Bauteilabmessungen in '''TVAR-Variablen''' speichern. | Mit dem CABD - Werkzeugen kann man Bauteilabmessungen in '''TVAR-Variablen''' speichern. | ||
| Zeile 152: | Zeile 161: | ||
tvar name 'tu_v' val 50 cmnt 't-Unterflansch' | tvar name 'tu_v' val 50 cmnt 't-Unterflansch' | ||
tvar name 'ts_v' val 40 cmnt 't-Stege' | tvar name ''''ts_v'''' val 40 cmnt 't-Stege' | ||
Diese Variabel werden dann bei der Querschnittsdefinition eingesetzt: | Diese Variabel werden dann bei der Querschnittsdefinition eingesetzt: | ||
qsp nr 1 y 0 z '=-#to_v/2' refp OL refd ~OR mnr 0 | qsp nr 1 y 0 z ''''=-#to_v/2'''' refp OL refd ~OR mnr 0 | ||
Der Konstruktionspunkt 1 liegt y=0 und z=#to_v/2 unterhalb von OL in Richtung OR (absolute Koordinaten). Das geht ganz gut, da hier die Variable nur durch 2 dividiert wird. Man beachte die Hochkommas und das Gleichheitszeichen. | Der Konstruktionspunkt 1 liegt y=0 und z=#to_v/2 unterhalb von OL in Richtung OR (absolute Koordinaten). Das geht ganz gut, da hier die Variable nur durch 2 dividiert wird. Man beachte die Hochkommas und das Gleichheitszeichen. | ||
| Zeile 162: | Zeile 171: | ||
Muss man mit den tvar-Variablen wirklich kompliziertere Rechenoperationen ausführen, wird es verzwackt. | Muss man mit den tvar-Variablen wirklich kompliziertere Rechenoperationen ausführen, wird es verzwackt. | ||
1. kann | 1. kann man '''[[C Funktionen|FUN]]'''ktionen einsetzten: | ||
let#y_qsp '=FUN(ts_v,((#ue+#ts_v/2))/cos(10))' | let#y_qsp '=FUN(ts_v,((#ue+'''#ts_v'''/2))/cos(10))' beachte '=FUN ! keine Kleinschreibung $ SOFiSTiK rechnet mit Altgrad | ||
qsp nr 13 y #y_qsp(#ts_v) z 0 refp 11 refd ~12 mnr 0 | qsp nr 13 y #y_qsp(#ts_v) z 0 refp 11 refd ~12 mnr 0 | ||
| Zeile 179: | Zeile 188: | ||
qsp nr 13 y #99 z 0 refp 11 refd ~12 mnr 0 | qsp nr 13 y #99 z 0 refp 11 refd ~12 mnr 0 | ||
3. beachte | |||
Bei der Durchführung der Interpolation gehen LET-Variablen in diesen Ausdrücken verloren. Entweder man löst dies über STO-Variablen: | |||
tvar name 'beff_l' val 1,49 cmnt 'mitwirkende Breite' | |||
sto#y12 0 | |||
sto#y13 #y12-4972 also sto und eine konkrete Zahl | |||
neff nr 1.... ymax '=#y13+(#beff_l*1000)' | |||
oder | |||
tvar name 'ymax' val -4972 cmnt 'Betonbreite' | |||
neff nr 1.... ymax '=#ymax+(#beff_l*1000)' | |||
4. das Spiegeln | |||
man kann sehr bequem Punkte (Spannungspunkte) spiegeln: | |||
qsp nr refp refd mnr=0 | |||
21 -12 12 Punkt Nr. 21 entsteht durch die Spiegelung des Punktes 12 an der z-Achse | |||
s. AQUA Handbuch Abschn. 3.31.1 | |||
s. C:\Glossar\A\AQUA\Parametrisierte Querschnitte | |||
== gutes Beispiel == | |||
s. Beispiele: csm28_suspension_bridge_real.dat | |||
[[Datei:Querschnittsvariablen.jpg|mini|rechts|parametrisierter Querschnitt]] | |||
== Variantenuntersuchung == | == Variantenuntersuchung == | ||
| Zeile 189: | Zeile 231: | ||
Dr. Niggl hat das Modul Grasshopper vorgestellt. Das war sehr beeindruckend, wie er mit diesem Programm visuell und parametrisiert Strukturen erzeugen kann. | Dr. Niggl hat das Modul Grasshopper vorgestellt. Das war sehr beeindruckend, wie er mit diesem Programm visuell und parametrisiert Strukturen erzeugen kann. | ||
[[Kategorie:Allgemeines zu CADINP]] | [[Kategorie:Allgemeines zu CADINP]] | ||
[[Kategorie:AQUA]] | |||
[[Kategorie:SOFiMSHC]] | |||
Aktuelle Version vom 19. Juli 2023, 14:00 Uhr
Vorbemerkungen
Mittels der Parametrisierung (bei textbasierter Eingabe) lassen sich schnell und sicher die Eingangsgrößen einer Berechnung varieren. Wesentlich ist dabei, dass man wirklich an allen Stellen, wo der Paramter in die Berechnung eingeht, auch tatsählich diesen Parameter verwendet. Die Parametrisierung ist die Voraussetzung für Variantenuntersuchungen.
Aufgepasst! Man beachte auch, dass eine lokale LET-Variable eine gleichnamige globale STO-Variable überschreibt!!!
Da das Programm keine Warnung bei der Überschreibung einer STO-Variable gibt, kann man natürlich echten Blödsinn fabrizieren. 👀
Wenn zum Beispiel sto#w 65 die Brückenschiefe definiert und man zwischendurch mal die Windlast mit let#w 2,6 festlegt, dann ist es passiert. Falls man anschließend sin(#w) verwendet, um aus der Brückenschiefe etwas abzuleiten, so ist das Ergebnis sehr wunderlich! Hier hilft, für die Variablen länger Namen zu verwenden: #w_schiefe und #wind.
Das klingt alles ganz gut???! hat aber auch seine Haken. Man kann z.Bsp. eine Variable mit sto#variable in die Datenbank schreiben. Dann verwendet man diese...alles prima. Aber wir Statiker wollen ja alles x-mal ändern. Also verwenden wir eine andere Variable sto#variable_neu! Leider haben wir zwischenzeitlich vergessen, dass wir die alte Variable an mehreren Stellen verwendet haben. Nun kommt das große Staunen. 🤔 regelmäßig die DATENBANK LÖSCHEN!!!!
Da man bei integralen Brücken die unterschiedlichen Grenzwerte Bodensteifigkeiten betrachten muss, sind diese Bauwerke nur mittels Parametrisierung berechenbar.
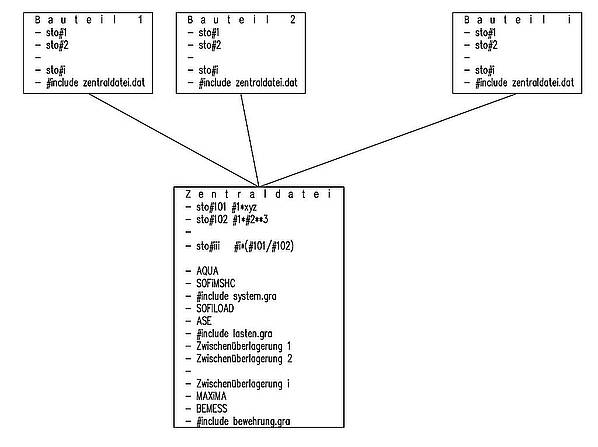
Parametrisierung bei ähnlichen Bauteilen
Bei ähnlichen Bauteilen (Tunnelquerschnitte, Schächte, Tröge, Fertigteile, Lärmschutzwände...) bietet es sich an, die Berechnung in einer Zentraldatei durchzuführen. Neben der Geometrie werden auch die Lasten über Parameter erfasst. Für jedes einzelne Bauteil wird dann nur eine kleine Steuerdatei erzeugt, in welcher die konkreten Parameter definiert werden. Diese Arbeitsweise hat einige Vorteile, bedarf aber auch einer gewissen Konsequenz und einer intensiven Kontrolle.
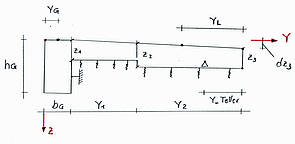
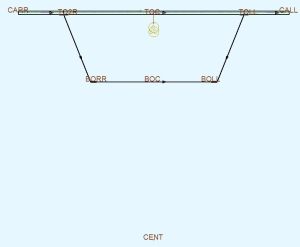
Skizzen
Grundlage der Parametrisierung sind Skizzen...gut aufheben!
Definition und Kontrollausgabe
prog template kopf Parameter
- sto#y_teller 0.75 $ Abstand der Telleranker vom Schrammbord
- sto#styp 'B' $ Art der Einfügung des Querschnitts auf die Strukturlinie
ende
Kontrollausgabe:
txa Abstand der Telleranker vom Bord = #(#y_teller,5.3) m
Besonderheiten bei Textvariablen
Die vereinbarten Textvariabel (sto#styp 'B') sind immer 8 Zeichen lang. Es darf aber (in diesem Fall) nur das erste Zeichen verwendet werden. Deshalb muss bei der Verwendung der Textvariabel #styp das konkret zu verwendete Zeichen benannt werden: styp=#styp(1:1) Durch diesen Aufruf wird nur das B übergeben.
Alternativ kann man auch ganz Eingabezeilen mittels #define vorgeben. Bei Plattenbalkenkonstruktionen geht z.Bsp.
#define orto=GRP2 31,32 QEMX 0.005 QUEA 0.005
Um dann später im ASE
$(orto)
und im CSM
steu ASE text "$(orto)"
zu schreiben.
Anwendung
!*!Label Telleranker
$ Knoten an der OK der Platte
loop#i #maxnr3
let#nr #i+1
spt nr 200+#nr x #x_teller(#nr) y #bg+#ly-#y_teller z #dz3*((#y2-#y_teller)/#y2) nx 0 ny 0 nz 1 sx 1 sy 0 sz 0
sptp typ kf grp 2 ref 300+#nr $ Kopplung auf den Lagerknoten
endloop
$ Knoten an der UK der Platte für die Telleranker
loop#i #maxnr3
let#nr #i+1
spt nr 300+#nr x #x_teller(#nr) y #bg+#ly-#y_teller z #z2-#z_teller fix 'pypz' nx 0 ny 0 nz 1 sx 1 sy 0 sz 0
endloop
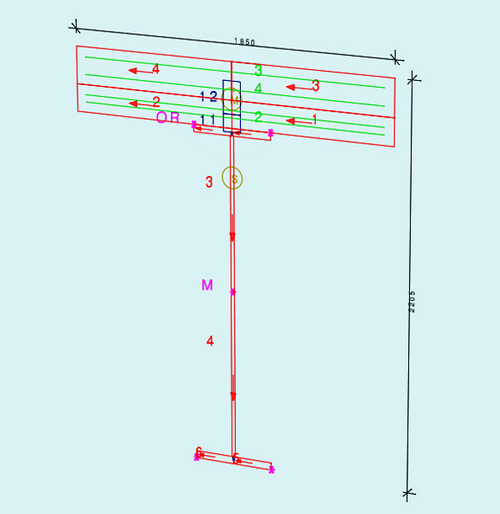
Parametrisierung eines Verbundquerschnitte
Im Stahlverbundbau ist Parametrisierung ein "Muss". Besonders die Blechdicken und die Trägerhöhen dienen der Anpassung des Widerstands an die Beanspruchung. Man definiert einen Block (hier qt), in welchem ein Stahlverbundquerschnitt in Abhängigkeit der Variable #htr generiert wird. Die Generierung der vielen unterschiedlich hohen Träger erfolgt dann mittels einer Schleife über ein Feld:
!*!Label restliche Träger
let#h 1452,1124,860,657,514,428,400,429,515,659,863,1128,1457,1850 $ Höhen der einzelnen Stahlträger
loop#i h
let#qnr #qnr+1 $ Querschnittsnummer
let#htr #h(#i)
#include qt
endloop
Querschnittsdefinition
Mit der nachstehenden Eingabe wird der komplette Stahlverbundquerschnitt definiert:
QNR #qnr mnr #mnr BEZ 'LT-Nr. #qnr'
BA 1 BEZ 'Stahlträger ohne Platte'
$ Stahlträger über Bleche
blec nr ya za ye ze d mnr=#mnr
1 #y1 #z1 #y2 #z2 #o
2 #y2 #z2 #y3 #z3 #o
3 #y4 #z4 #y5 #z5 #s
4 #y5 #z5 #y6 #z6 #s
5 #y7 #z7 #y8 #z8 #u
6 #y8 #z8 #y9 #z9 #u
$ Schweißnähte
LNAH NR YA ZA YE ZE D MNR=2
1 #y2 #z2 #y4 #z4 #sn
2 #y6 #z6 #y8 #z8 #sn
QSP nr y z mnr=#mnr
'OL' #y1 #z1-#o/2
'OR' #y3 #z3-#o/2
'UL' #y7 #z7+#u/2
'UR' #y9 #z9+#u/2
'M' #y5 #z5
BA 10 BEZ 'Stahlträger + 1. Platte'
$ 1. Betonplatte
$ Punkte auf den Mittellinien der Wände
$ Mindestbewehrung in den Rängen m1 bis m4
let#as1 9 $7.7*((#bl+#br)/1000) $ 7.7cm2/1000mm d=14 a=20
let#das1 14
wand nr ya za ye ze d mnr
1 #bl #z11 0 #z11 #db1 11
2 0 #z11 -#br #z11 #db1 11
lbew nr ya za ye ze rang as=#as1 d=#das1 a=#br+#bl tors=akti mbw=3
1 #bl-#cbew #db2+#cbew -#br+#cbew #db2+#cbew f1
2 #bl-#cbew #db2+#db1-#cbew -#br+#cbew #db2+#db1-#cbew f2
$ untere Verdübelung
LNAH NR YA ZA YE ZE D MNR=4
11 #y2 #z2 #y11 #z11 -100 $ Schubverdübelung Stahlräger- 1. Platte
BA 20 BEZ '+ 2. Platte'
let#as2 9
let#das2 14
$ Ortbetonplatte
wand nr ya za ye ze d mnr
3 #bl #z12 0 #z12 #db2 12
4 0 #z12 -#br #z12 #db2 12
lbew nr ya za ye ze rang as=#as2 d=#das2 a=#br+#bl tors=akti mbw=3
3 #bl-#cbew #cbew -#br+#cbew #cbew f3
4 #bl-#cbew #db2-#cbew -#br+#cbew #db2-#cbew f4
$ obere Verdübelung
LNAH NR YA ZA YE ZE D MNR=5
12 #y11 #z11 #y12 #z12 -100 $ Schubverdübelung zwischen den beiden Platte
Ggf. sind noch nichtmitwirkende Plattenbereiche zu definieren.
gevouteter Brückenträger
Mit den unterschiedlich hohen Stahlverbundquerschnitten ergibt sich ein Längsträger mit einer Voutung.
Mit dem CABD kann man das aber noch etwas eleganter erledigen.
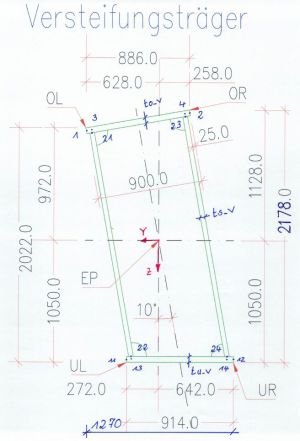
Parametriesierung mit CABD
Mit dem CABD - Werkzeugen kann man Bauteilabmessungen in TVAR-Variablen speichern.
tvar name 'to_v' val 50 cmnt 't-Oberflansch'
tvar name 'tu_v' val 50 cmnt 't-Unterflansch'
tvar name 'ts_v' val 40 cmnt 't-Stege'
Diese Variabel werden dann bei der Querschnittsdefinition eingesetzt:
qsp nr 1 y 0 z '=-#to_v/2' refp OL refd ~OR mnr 0
Der Konstruktionspunkt 1 liegt y=0 und z=#to_v/2 unterhalb von OL in Richtung OR (absolute Koordinaten). Das geht ganz gut, da hier die Variable nur durch 2 dividiert wird. Man beachte die Hochkommas und das Gleichheitszeichen.
Muss man mit den tvar-Variablen wirklich kompliziertere Rechenoperationen ausführen, wird es verzwackt.
1. kann man FUNktionen einsetzten:
let#y_qsp '=FUN(ts_v,((#ue+#ts_v/2))/cos(10))' beachte '=FUN ! keine Kleinschreibung $ SOFiSTiK rechnet mit Altgrad
qsp nr 13 y #y_qsp(#ts_v) z 0 refp 11 refd ~12 mnr 0
Der Variablen #y_qsp wird der Funktionswert zugeiwesen. Hier nun ohne '=#ts_v' sondern lediglich #ts_v.
Der Konstruktionspunkt 13 liegt y=#y_qsp und z=0 von 11 in Richtung 13. 😂
2. kann man auch eine Variable berechnen:
let#99 (#ue+#ts_v/2)/cos(10)
auch wieder ohne '=...'
qsp nr 13 y #99 z 0 refp 11 refd ~12 mnr 0
3. beachte
Bei der Durchführung der Interpolation gehen LET-Variablen in diesen Ausdrücken verloren. Entweder man löst dies über STO-Variablen:
tvar name 'beff_l' val 1,49 cmnt 'mitwirkende Breite'
sto#y12 0
sto#y13 #y12-4972 also sto und eine konkrete Zahl
neff nr 1.... ymax '=#y13+(#beff_l*1000)'
oder
tvar name 'ymax' val -4972 cmnt 'Betonbreite'
neff nr 1.... ymax '=#ymax+(#beff_l*1000)'
4. das Spiegeln man kann sehr bequem Punkte (Spannungspunkte) spiegeln:
qsp nr refp refd mnr=0
21 -12 12 Punkt Nr. 21 entsteht durch die Spiegelung des Punktes 12 an der z-Achse
s. AQUA Handbuch Abschn. 3.31.1
s. C:\Glossar\A\AQUA\Parametrisierte Querschnitte
gutes Beispiel
s. Beispiele: csm28_suspension_bridge_real.dat
Variantenuntersuchung
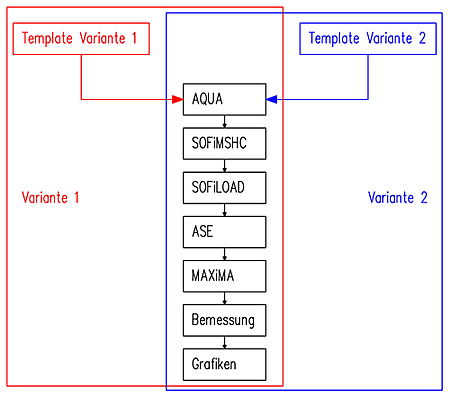
Statiker müssen immer wieder Varianten untersuchen. Besonders im Grundbau und bei integralen Brücken, aber auch in den anderen Bereichen der Tragwerksplanung, steht häufig die Frage: "...und wenn nun die Eingangsgröße XYZ den Wert 123 hat?". Für die Lösung dieser Aufgabenstellung sollte man die Berechnung parametrisieren und den Ablauf entsprechend des unten dargestellten Schemas organisieren. Das hat den Vorteil, dass man im Zuge der häufig erforderlichen Überarbeitung immernoch den Überblick bewahrt.
Am besten gibt man den Teilaufgaben entsprechend aussagekräftige Namen und benutzt vor allem die Kommentare im TEDDY.
Grasshopper
Dr. Niggl hat das Modul Grasshopper vorgestellt. Das war sehr beeindruckend, wie er mit diesem Programm visuell und parametrisiert Strukturen erzeugen kann.